
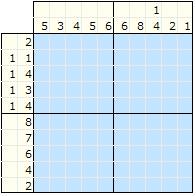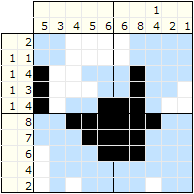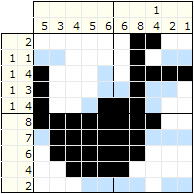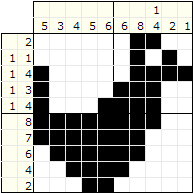
Obrazki logiczne to łamigłówka polegająca na zaczernianiu pól diagramu, zaczernione pola utworzą rysunek. To które pola trzeba zaczernić wskazują liczby obok diagramu. Liczby z lewej strony każdego wiersza określają, ile grup czarnych pól jest w danym rzędzie i ile czarnych pól jest w każdej grupie. Dla przykładu liczby „1,4” (w trzecim rzędzie) oznaczają dwie grupy: pierwsza jest złożona z jednego, a druga z czterech czarnych pól. Wyodrębnienie 2 kolejnych liczb świadczy o tym, że pomiędzy grupami czarnych pól występuje przynajmniej jedno wolne (białe) pole. Analogicznie jest z liczbami u góry diagramu.
Obrazki czarno białe są klasyczną wersją ale czasami można spotkać wersję z wieloma kolorami, w której pola diagramu koloruje się zgodnie z kolorem liczb. Pola z dwoma różnymi kolorami nie muszą mieć białego pola pomiędzy sobą.
Za ojca Malowania Liczbami uznaje się japońskiego grafika Non Ishida, który w 1987 roku w Tokio wygrał konkurs polegający na ułożeniu obrazu z zapalonych świateł w wieżowcu. Pomysł gry powstał przy próbie zapisu na papierze obrazka malowanego na wieżowcu. W tym samym czasie japoński profesor Tetsuya Nishio wpadł na identyczny pomysł.
Pierwsze łamigłówki zostały opublikowane w japońskich magazynach szaradziarskich. W 1988 roku Non Ishida, w Japonii opublikował trzy obrazki logiczne pod nazwą „Window Art. Puzzles” W 1990 roku, w Wielkiej Brytanii, James Dalgety spopularyzował Obrazki Logiczne pod nazwą „Nonograms” - publikując je w The Sunday Telegraph.
Pierwsza książka z Obrazkami Logicznymi ukazała się w Japonii, w 1993 roku, jej autorem był Nin Ishida. W niedługim czasie książki takie zaczęły ukazywać się w innych krajach. Pierwsze gry elektroniczne wyprodukowała firma Nintendo w 1995 roku - (platforma Game Boy) pod nazwą “Picross”.
W 1998 roku The Sunday Telegraph ogłosił konkurs na nową nazwę dla Obrazków Logicznych - wygrała nazwa „Griddlers”. Dzisiaj magazyny z Obrazkami Logicznymi publikowane są w wielu krajach świata.
W Polsce łamigłówkę tę spopularyzowała gazeta Wiedza i Życie – publikując przez wiele lat Obrazki Logiczne.
1 stycznia 2006 powstał polski serwis dla sympatyków Obrazków Logicznych: gameLO.net
Obrazki logiczne znane jest również jako: gameLO, Malowanie liczbami, Japońska Krzyżówka, Japońskie Puzzle, Japoński Obrazek, Crucipixel, Edel, FigurePic, Grafilogika, Griddlers, Hanjie, Illust-Logic, Japanese Crosswords, Japanese Puzzels, Kare Karala!, Logic Art, Logic Square, Logicolor, Logik-Puzzles, Logimage, Maľované krížovky, Nonograms, Oekaki Logic, Oekaki-Mate, Paint by Numbers, Paint Logic, Pic-a-Pix, Picross, Pixel Puzzles, Shchor Uftor, Tsunami, Zakókodované obrázky.
Najłatwiejszą metodą, używana na samym początku, jest metoda „Koniecznie pełne”. Należy ją używać do zaznaczenia możliwie największej ilości pól . Metoda ta polega na określeniu komórek, które muszą być pełne ze względu na zbyt ograniczone miejsce.
Rozpatrzmy przypadek:
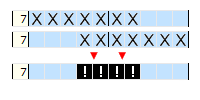
Wnioskowanie:
Te pola, które o należą do obu zbiorów na pewno są pełne.
Tę samą logikę można zastosować, gdy w rzędzie lub w kolumnie jest więcej grup.
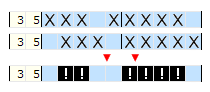
Wnioskowanie:
Ważnym jest aby brać pod uwagę tylko te pola, które pokryte są tym samym blokiem, a nie innym blokiem, innymi słowy tylko jeśli blok nakłada się na siebie to możemy wnioskować, że wspólne pola są pełne.
Ta metoda jest odwrotnością metody „Koniecznie pełne” i polega na określeniu pól, które na pewno będą puste, bo nie ma bloków, które mogły by je pokryć.
Rozpatrzmy przypadek:
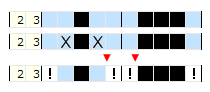
Wnioskowanie:
Ta metoda polega na dopasowywaniu bloków pól w miejsca, w których muszą się one znaleźć, bo nie da się ich ułożyć inaczej. Wolne pole położone gdzieś w środku rzędu może wymusić położenie większych bloków po jednej ze stron.
Cele, w które nie da się wcisnąć żadnego bloku, bo wszystkie bloki są za duże, będą na pewno puste.
Rozpatrzmy przypadek:
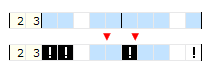
Wnioskowanie:
Czasami zdarza się, że odległość pełnego pola od brzegu jest mniejsza niż długość pierwszego (bądź ostatniego) bloku. W takim wypadku blok będzie rozciągał się na pełne pole i następne cele.
Rozpatrzmy przypadek:
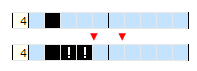
Wnioskowanie:
Tę metodę można wykorzystywać również środku rzędu jeśli traktować puste pole jak brzeg:
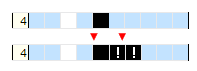
Wnioskowanie:
Pełne pola położone blisko siebie mogą być czasami łączone razem (na pewno należą do jednego bloku) lub rozdzielane (na pewno należą do innych bloków). Jeśli są 2 pełne pola oddzielone nieokreśloną jeszcze pole to będzie ono:
Przykład z pustym polem:

Wnioskowanie:
Przykład z pełnym polem:

Wnioskowanie:
Bardzo ważne jest aby skończone bloki oznaczać pustymi polami na końcach. Pozwala to na łatwiejsze wykorzystywanie innych metod, na przykład „Wciskania”.
Jest to specjalna odmiana metody “Koniecznie puste”. Nazwa pochodzi od rtęci, która to naturalnie odpycha się od krawędzi pojemnika.
Jeśli pełne pole odsunięte jest od brzegu o tyle pól ile ma pierwszy blok to pierwsze pole w tym rzędzie będzie puste. Dzieje się tak dlatego, że blok nie może być dosunięty maksymalnie, bo byłby za długi.
Rozpatrzmy przypadek:
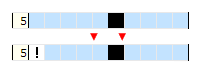
Wnioskowanie:
Do rozwiązania trudniejszych obrazków trzeba wykorzystywać metodę „nie wprost”. Kiedy wszystkie proste metody zawiodą potrzebna jest dedukcja obejmująca więcej kolumn lub rzędów. Metoda ta zakłada, że komórka musi być pełna, ponieważ gdyby była pusta to w innych komórkach występował by błąd i odwrotnie.
Trudność tej metody polega na tym, że trzeba sobie wyobrazić kolejne kroki, ale nie powinno się ich zapisywać.
Przykład, w którym zakładamy, że pole jest pełne:
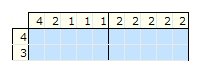
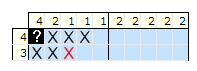
Zakładamy, że pierwsze pole w pierwszym rzędzie jest pełne.
Wnioskowanie:
Przykład, w którym zakładamy, że pole jest pełne:
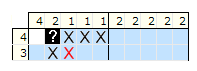
Zakładamy, że drugie pole w pierwszym rzędzie jest pełne.
Wnioskowanie:
Przykład, w którym zakładamy, że pole jest pełne:
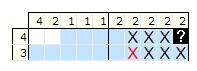
Zakładamy, że pole 10 w pierwszym rzędzie jest pełne.
Wnioskowanie:
Przykład, w którym zakładamy, że pole jest pełne:
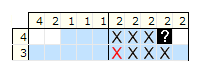
Zakładamy, że pole 9 w pierwszym rzędzie jest pełne.
Wnioskowanie:
W ten sposób można analizować większą liczbę rzędów, lub kolumn – wszystko zależy od wprawy gracza. Podobnie można postępować zakładając, że pole jest puste.
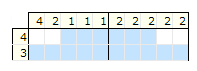
Problemem przy używaniu tej metody jest fakt, że nie wiadomo, od którego pustego pola zacząć.
Najlepiej zaczynać od:
Jest to najtrudniejsza, wymagająca dużo wprawy metoda, ale wiele obrazków możemy rozwiązać tylko dzięki niej.
Jest to najtrudniejsza, wymagająca dużo wprawy metoda, ale wiele obrazków możemy rozwiązać tylko dzięki niej.
Aby dowiedzieć się więcej o logicznych obrazkach przejdź na stronę Wikipedii: